Why do you need ANN? | Background

Elastic Search, Faiss and etc. all adopted their own approximate nearest neighbor search algorithms to deal with vector search among the huge scale of corpus. During my near research for my final-year project (FYP), which is to develop a production-level distributed search engine, I have looked into vector search, inverted index and Learning-to-Rank, for my main and the most used features — searching .

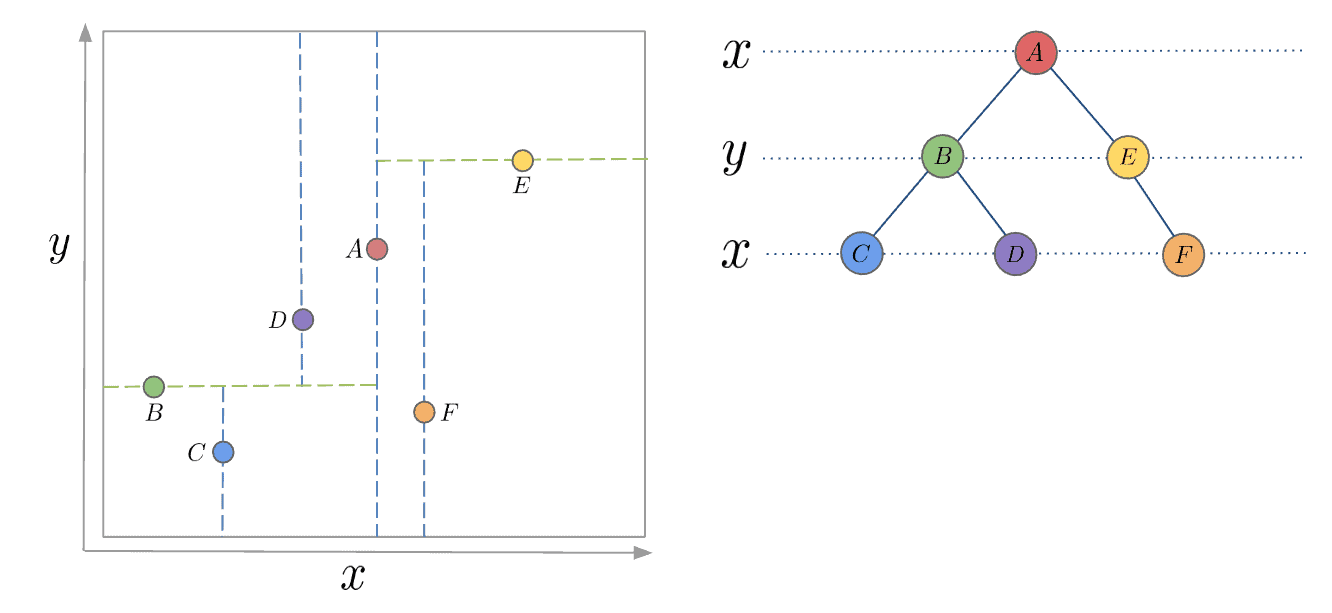
My FYP intrigues me into exploring acceleration of vector search. Based on my previous knowledge, in game / navigation, in order to speed up the search process, a common solution is to use K-D Trees, which recursively partition orthognal axies to construct a tree structure so that it only takes time complexity O(log n) to search, referring to Fig. 1. However, even though partitioning sounds intuitive, it does not work well when the dimensions grows explosively into 256 or 1024, which will bring a long time to partition into all k dimensions. Therefore, I am going to break down a few techiniques that are used for speeding up ANN process step by step.

This article is going to mostly cover vector search parts so we do not discuss about inverted index and Learning-to-Rank.

Starting from K-NN

It is not a secret that K-Nearest Neighbors (K-NN) is the simplest and most naive nearest neighbor search algorithm.

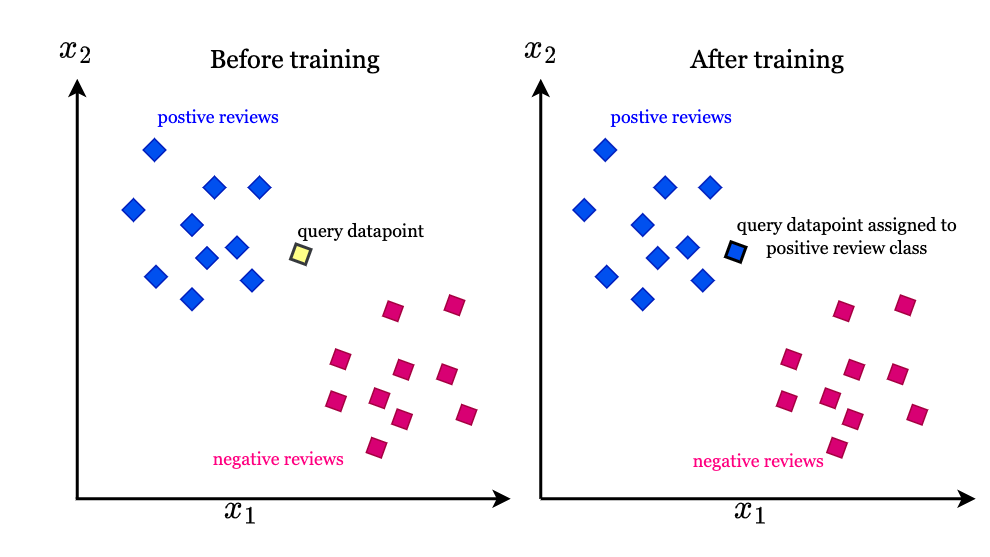
The principle of KNN algorithm is very simple: try to find the nearest neighbor of the query vector in the dataset. Usually these neighbors are belonged to a cluster so that it is able to put the query vector into specific class. This brutal algorithm’s time complexity is O(ND + Nlog(K)), where N denotes the number of vectors in the dataset and D denotes the dimension of the vectors, and Nlog(K) means to maintain the order of the candidate neighbors. Then KNN algorithm also can extend to find the nearest cluster to categorize each query, as shown in Fig. 2.

However, when the vector dimension explodes or the number of vectors vastly increases, K-NN algorithm reveals weakness in terms of its time complexity to inevitably calculate the euclidean distance for each and every vector in the dataset.

Anyway, I use Claude to generate a template for me to evaluate on ms-marco dataset, which you can find them appear in everywhere whenever it comes to searching, RAG or anything similar to information retrieval. Then I simulate K-NN algorithm by numpy through sorting euclidean distance for each queries. Then I calculate Recall, MRR and time cost taken by the algorithm.

import numpy as np
import time
from sentence_transformers import SentenceTransformer
from datasets import load_dataset
from tqdm import tqdm

print("Loading model...")
model = SentenceTransformer('sentence-transformers/msmarco-MiniLM-L-6-v3')

# Load MS MARCO dataset
print("\nLoading dataset...")
dataset = load_dataset('ms_marco', 'v1.1', split='train[:10000]')

# Extract queries and build qrels
queries = []
qrels = {}
corpus = {}

print("\nProcessing data...")
for idx, item in enumerate(tqdm(dataset, desc="Processing items")):
    # Check if there are answers
    if item['answers'] and len(item['answers']) > 0:
        query_text = item['query']
        
        # Extract relevant passages
        relevant_passages = []
        passages = item['passages']
        
        # Add all passages to corpus (v1.1 doesn't have passage_id, need to create our own)
        for i in range(len(passages['passage_text'])):
            ptext = passages['passage_text'][i]
            is_selected = passages['is_selected'][i]
            
            # Create unique passage ID using query_id and passage index
            pid = f"{item['query_id']}_{i}"
            
            # Add to corpus
            if pid not in corpus:
                corpus[pid] = ptext
            
            # If it's a relevant passage, record it
            if is_selected == 1:
                relevant_passages.append(pid)
        
        # Only keep queries with relevant passages
        if relevant_passages:
            queries.append(query_text)
            qrels[len(queries) - 1] = set(relevant_passages)

print(f"\n{'='*50}")
print(f"Data Statistics:")
print(f"{'='*50}")
print(f"Queries: {len(queries)}")
print(f"Corpus: {len(corpus)}")
print(f"Average relevant docs per query: {np.mean([len(v) for v in qrels.values()]):.2f}")
print(f"{'='*50}")

# Prepare for encoding
corpus_ids = list(corpus.keys())
corpus_texts = list(corpus.values())

print("\nEncoding corpus...")
corpus_embeddings = model.encode(
    corpus_texts, 
    batch_size=128, 
    show_progress_bar=True,
    convert_to_numpy=True
)

print("\nEncoding queries...")
query_embeddings = model.encode(
    queries, 
    batch_size=128, 
    show_progress_bar=True,
    convert_to_numpy=True
)

# Normalize for cosine similarity
print("\nNormalizing embeddings...")
corpus_embeddings = corpus_embeddings / np.linalg.norm(corpus_embeddings, axis=1, keepdims=True)
query_embeddings = query_embeddings / np.linalg.norm(query_embeddings, axis=1, keepdims=True)

# KNN search
def knn_search(query_vecs, corpus_vecs, k=10):
    """Efficient KNN search using numpy"""
    scores = np.dot(query_vecs, corpus_vecs.T)
    top_k_idx = np.argsort(scores, axis=1)[:, -k:][:, ::-1]
    top_k_scores = np.take_along_axis(scores, top_k_idx, axis=1)
    return top_k_scores, top_k_idx

print("\nPerforming retrieval...")
retrieval_start = time.time()
scores, indices = knn_search(query_embeddings, corpus_embeddings, k=10)
retrieval_time = time.time() - retrieval_start
print(f"Search completed in {retrieval_time:.4f} seconds")

# Evaluation
print("\nCalculating evaluation metrics...")
mrr = 0.0
recall_at_10 = 0.0
precision_at_10 = 0.0
valid_queries = 0

for q_idx in tqdm(range(len(queries)), desc="Evaluating"):
    if q_idx not in qrels:
        continue
    
    relevant = qrels[q_idx]
    retrieved = [corpus_ids[idx] for idx in indices[q_idx]]
    
    # Calculate MRR
    for rank, doc_id in enumerate(retrieved, 1):
        if doc_id in relevant:
            mrr += 1.0 / rank
            break
    
    # Calculate Recall@10
    hits = len(set(retrieved) & relevant)
    recall_at_10 += hits / len(relevant)
    
    # Calculate Precision@10
    precision_at_10 += hits / len(retrieved)
    
    valid_queries += 1

# Average metrics
mrr /= valid_queries
recall_at_10 /= valid_queries
precision_at_10 /= valid_queries

print(f"\n{'='*50}")
print(f"Evaluation Results:")
print(f"{'='*50}")
print(f"Number of evaluated queries: {valid_queries}")
print(f"MRR@10:        {mrr:.4f}")
print(f"Recall@10:     {recall_at_10:.4f}")
print(f"Precision@10:  {precision_at_10:.4f}")
print(f"{'='*50}")

Results

Loading dataset...

Processing data...
Processing items: 100%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 10000/10000 [00:00<00:00, 13605.77it/s]

==================================================
Data Statistics:
==================================================
Queries: 9690
Corpus: 80128
Average relevant docs per query: 1.12
==================================================

Encoding corpus...
Batches: 100%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 626/626 [00:39<00:00, 15.77it/s]

Encoding queries...
Batches: 100%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 76/76 [00:00<00:00, 103.18it/s]

Normalizing embeddings...

Performing retrieval...
Search completed in 33.6314 seconds

Calculating evaluation metrics...
Evaluating: 100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 9690/9690 [00:00<00:00, 132921.27it/s]

==================================================
Evaluation Results:
==================================================
Number of evaluated queries: 9690
MRR@10:        0.5874
Recall@10:     0.9541
Precision@10:  0.1057
==================================================

Experimental Setup

All experiments are conducted on RTX 2080 ti, Intel Core i5-12450H, 16GB RAM, Manjaro. We use python=3.10 and all latest library by the time of writing.

For the references

Then following searching, Elastic search uses HNSW algorithm